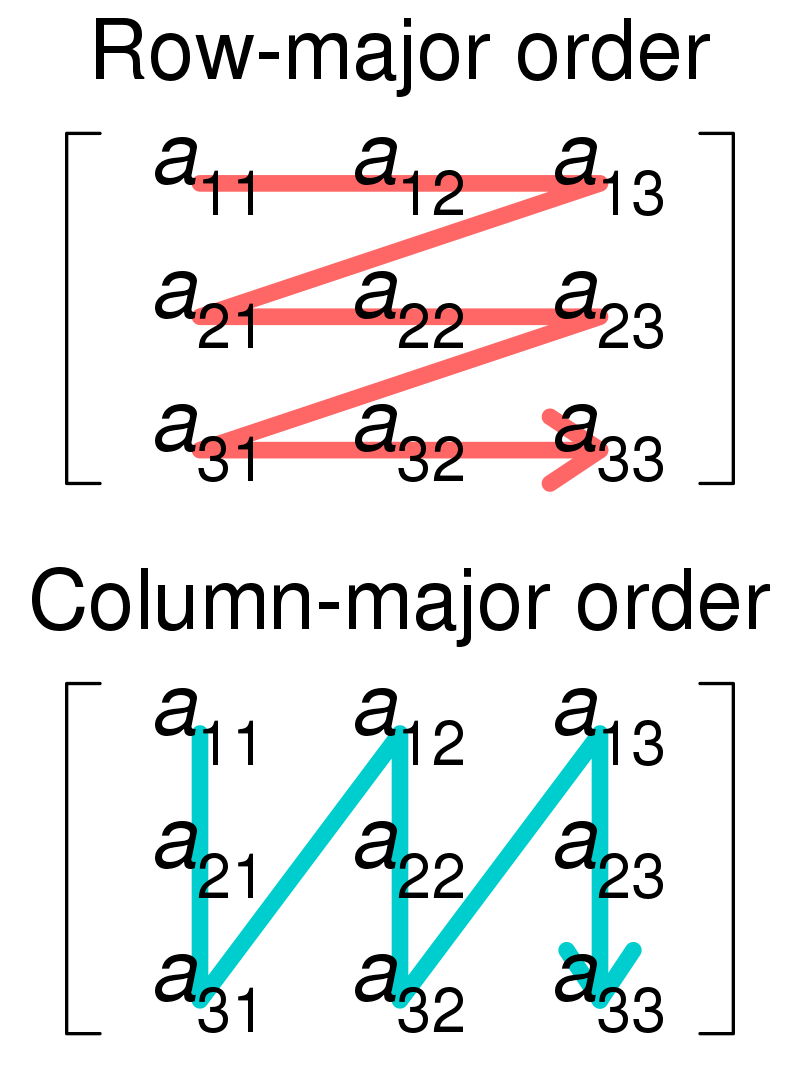
Kalyna State Matrix

• State Matrices use column major format similar to AES.

• These State matrices need not be of square size, they can contain - $128, 256, 512$ Bits and each cell in matrix stores $1$ Byte

  $$B_{128} = \begin{array}{|c|c|} \hline \mathtt{b_0} & \mathtt{b_8} \\ \hline \mathtt{b_1} & \mathtt{b_9} \\ \hline \mathtt{b_2} & \mathtt{b_{10}} \\ \hline \mathtt{b_3} & \mathtt{b_{11}} \\ \hline \mathtt{b_4} & \mathtt{b_{12}} \\ \hline \mathtt{b_5} & \mathtt{b_{13}} \\ \hline \mathtt{b_6} & \mathtt{b_{14}} \\ \hline \mathtt{b_7} & \mathtt{b_{15}} \\ \hline \end{array} \hspace{5mm} B_{256} = \begin{array}{|c|c|c|c|}\hline \mathtt{b_0} & \mathtt{b_8} & \mathtt{b_{16}} & \mathtt{b_{24}} \\ \hline \mathtt{b_1} & \mathtt{b_9} & \mathtt{b_{17}} & \mathtt{b_{25}} \\ \hline \mathtt{b_2} & \mathtt{b_{10}} & \mathtt{b_{18}} & \mathtt{b_{26}} \\ \hline \mathtt{b_3} & \mathtt{b_{11}} & \mathtt{b_{19}} & \mathtt{b_{27}} \\ \hline \mathtt{b_4} & \mathtt{b_{12}} & \mathtt{b_{20}} & \mathtt{b_{28}} \\ \hline \mathtt{b_5} & \mathtt{b_{13}} & \mathtt{b_{21}} & \mathtt{b_{29}} \\ \hline \mathtt{b_6} & \mathtt{b_{14}} & \mathtt{b_{22}} & \mathtt{b_{30}} \\ \hline \mathtt{b_7} & \mathtt{b_{15}} & \mathtt{b_{23}} & \mathtt{b_{31}} \\ \hline \end{array}$$

  $$B_{512} = \begin{array}{|c|c|c|c|c|c|c|c|} \hline \mathtt{b_0} & \mathtt{b_8} & \mathtt{b_{16}} & \mathtt{b_{24}} & \mathtt{b_{32}} & \mathtt{b_{40}} & \mathtt{b_{48}} & \mathtt{b_{56}} \\ \hline \mathtt{b_1} & \mathtt{b_9} & \mathtt{b_{17}} & \mathtt{b_{25}} & \mathtt{b_{33}} & \mathtt{b_{41}} & \mathtt{b_{49}} & \mathtt{b_{57}} \\ \hline \mathtt{b_2} & \mathtt{b_{10}} & \mathtt{b_{18}} & \mathtt{b_{26}} & \mathtt{b_{34}} & \mathtt{b_{42}} & \mathtt{b_{50}} & \mathtt{b_{58}} \\ \hline \mathtt{b_3} & \mathtt{b_{11}} & \mathtt{b_{19}} & \mathtt{b_{27}} & \mathtt{b_{35}} & \mathtt{b_{43}} & \mathtt{b_{51}} & \mathtt{b_{59}} \\ \hline \mathtt{b_4} & \mathtt{b_{12}} & \mathtt{b_{20}} & \mathtt{b_{28}} & \mathtt{b_{36}} & \mathtt{b_{44}} & \mathtt{b_{52}} & \mathtt{b_{60}} \\ \hline \mathtt{b_5} & \mathtt{b_{13}} & \mathtt{b_{21}} & \mathtt{b_{29}} & \mathtt{b_{37}} & \mathtt{b_{45}} & \mathtt{b_{53}} & \mathtt{b_{61}} \\ \hline \mathtt{b_6} & \mathtt{b_{14}} & \mathtt{b_{22}} & \mathtt{b_{30}} & \mathtt{b_{38}} & \mathtt{b_{46}} & \mathtt{b_{54}} & \mathtt{b_{62}} \\ \hline \mathtt{b_7} & \mathtt{b_{15}} & \mathtt{b_{23}} & \mathtt{b_{31}} & \mathtt{b_{39}} & \mathtt{b_{47}} & \mathtt{b_{55}} & \mathtt{b_{63}} \\ \hline \end{array}$$

  ---

Substitution Box $(\pi)$

• We need to apply the following 8-Bit S-Box $(\pi:\{0,1\}^8 \to \{0,1\}^8)$ over each byte of a column the following way

  $$b_i \to \pi_{(i\bmod4)}[b_i] \hspace{3mm}i \in [0,7]$$

  $$\begin{array}{|c|} \hline \mathtt{b_0} \\ \hline \mathtt{b_1} \\ \hline \mathtt{b_2} \\ \hline \mathtt{b_3 }\\ \hline \mathtt{b_4 } \\ \hline \mathtt{b_5} \\ \hline \mathtt{b_6} \\ \hline \mathtt{b_7} \\ \hline \end{array}\to \begin{array}{|c|} \hline \mathtt{\pi_0[b_0]} \\ \hline \mathtt{\pi_1[b_{1}]} \\ \hline \mathtt{\pi_2[b_{2}]} \\ \hline \mathtt{\pi_3[b_{3}]} \\ \hline \mathtt{\pi_0[b_4]} \\ \hline \mathtt{\pi_1[b_{5}]} \\ \hline \mathtt{\pi_2[b_{6}]} \\ \hline \mathtt{\pi_3[b_{7}]} \\ \hline \end{array}$$

Shift Rows $(\tau)$

• This Byte Wise Permutation layer in the Round Function is used to add Diffusion
  • Diffusion - Used to hide the relationship between the Ciphertext and the Plaintext

• We do Right Circular Shift for the rows the following way

• Right Circular Shift - Move the Right Most Byte of the row to the left Most and push the remaining bytes to the right

• The amount of Left Shift depends on the Row Number $(r)$ and Block Size $(l)$ or Number of Block Rows $(c)$ - ensure that each row of the array is moved by a different number of byte positions

  $$\text{shift} = \left\lfloor\frac{r\times l}{512} \right\rfloor = \left\lfloor\frac{r\times c}{8}\right\rfloor$$

Mix Columns $(\psi)$

• Mixes each column of the State Matrix

• We do a Matrix-Vector Multiplication with the Column $C = [b_0,b_1,b_2,b_3,b_4,b_5,b_6,b_7]$ and an MDS Matrix $M$ to give the resultant column vector $C = [d_0,d_1,d_2,d_3,d_4,d_5,d_6,d_7]$ that is within a Galois Field $GF(2^8)$

  $$\begin{bmatrix} \mathtt{01} & \mathtt{01} & \mathtt{05} & \mathtt{01} & \mathtt{08} & \mathtt{06} &\mathtt{07} & \mathtt{04}\\ \mathtt{04} & \mathtt{01} & \mathtt{01} & \mathtt{05} & \mathtt{01} & \mathtt{08} & \mathtt{06} &\mathtt{07}\\ \mathtt{07} & \mathtt{04} & \mathtt{01} & \mathtt{01} & \mathtt{05} & \mathtt{01} & \mathtt{08} & \mathtt{06}\\ \mathtt{06} &\mathtt{07} & \mathtt{04} & \mathtt{01} & \mathtt{01} & \mathtt{05} & \mathtt{01} & \mathtt{08}\\ \mathtt{08} & \mathtt{06} &\mathtt{07} & \mathtt{04} & \mathtt{01} & \mathtt{01} & \mathtt{05} & \mathtt{01}\\ \mathtt{01} & \mathtt{08} & \mathtt{06} &\mathtt{07} & \mathtt{04} & \mathtt{01} & \mathtt{01} & \mathtt{05}\\ \mathtt{05} & \mathtt{01} & \mathtt{08} & \mathtt{06} &\mathtt{07} & \mathtt{04} & \mathtt{01} & \mathtt{01}\\ \mathtt{01} & \mathtt{05} & \mathtt{01} & \mathtt{08} & \mathtt{06} &\mathtt{07} & \mathtt{04} & \mathtt{01}\\ \end{bmatrix} \begin{bmatrix} b_0\\b_1\\b_2\\b_3 \\ b_4\\b_6\\b_6\\b_7 \end{bmatrix} = \begin{bmatrix}d_0\\d_1\\d_2\\d_3\\d_4\\d_5\\d_6\\d_7 \end{bmatrix}$$

• The inverse of this MDS Matrix is used while decrypting

  $$\begin{bmatrix} b_0\\b_1\\b_2\\b_3 \\ b_4\\b_6\\b_6\\b_7 \end{bmatrix} = \begin{bmatrix} \mathtt{AD} & \mathtt{95} & \mathtt{76} & \mathtt{A8} & \mathtt{2F} & \mathtt{49} &\mathtt{D7} & \mathtt{CA}\\ \mathtt{CA} & \mathtt{AD} & \mathtt{95} & \mathtt{76} & \mathtt{A8} & \mathtt{2F} & \mathtt{49} &\mathtt{D7} \\ \mathtt{D7} & \mathtt{CA} &\mathtt{AD} & \mathtt{95} & \mathtt{76} & \mathtt{A8} & \mathtt{2F} & \mathtt{49}\\ \mathtt{49} & \mathtt{D7} & \mathtt{CA} & \mathtt{AD} & \mathtt{95} & \mathtt{76} & \mathtt{A8} & \mathtt{2F}\\ \mathtt{2F} & \mathtt{49} & \mathtt{D7} & \mathtt{CA} &\mathtt{AD} & \mathtt{95} & \mathtt{76} & \mathtt{A8}\\ \mathtt{A8} & \mathtt{2F} & \mathtt{49} & \mathtt{D7} & \mathtt{CA} & \mathtt{AD} & \mathtt{95} & \mathtt{76}\\ \mathtt{76} & \mathtt{A8} & \mathtt{2F} & \mathtt{49} & \mathtt{D7} & \mathtt{CA} &\mathtt{AD} & \mathtt{95}\\ \mathtt{95} & \mathtt{76} & \mathtt{A8} & \mathtt{2F} & \mathtt{49} & \mathtt{D7} & \mathtt{CA} & \mathtt{AD}\\ \end{bmatrix} \begin{bmatrix}d_0\\d_1\\d_2\\d_3\\d_4\\d_5\\d_6\\d_7 \end{bmatrix}$$

$\operatorname{XOR}$ Round Key $(\kappa_l^{K_v})$

• In this operation we $\operatorname{XOR}$ the State matrix of block size $l$ bits with the $v^{th}$ Round Key $K_v$ derived from Key Expansion .

• The Round Keys have the same size as the Block even though the Master Key might differ in size. This is explained in Key Expansion in great detail.

• For a $128$ bit block size round key $K_{128}$ is defined the following way.

  $$K_{128} = \begin{array}{|c|c|} \hline \mathtt{k_0} & \mathtt{k_8} \\ \hline \mathtt{k_1} & \mathtt{k_9} \\ \hline \mathtt{k_2} & \mathtt{k_{10}} \\ \hline \mathtt{k_3} & \mathtt{k_{11}} \\ \hline \mathtt{k_4} & \mathtt{k_{12}} \\ \hline \mathtt{k_5} & \mathtt{k_{13}} \\ \hline \mathtt{k_6} & \mathtt{k_{14}} \\ \hline \mathtt{k_7} & \mathtt{k_{15}} \\ \hline \end{array} \hspace{5mm}$$

• The $\text{XOR}$ operation is done Byte wise the following way

Add Round Key $(\eta_l^{K_v})$

• Add Round Key is a new operation introduced in Kalyna unlike the previous ones mentioned which are extensions over $\text{AES}$ round operations. It is denoted by $\boxplus$.

• In this we again take the State Matrix of block size $l$ bits and combine with $v^{th}$ Round Key $K_v$ derived from Key Expansion by doing a addition modulus $2^{64}$

• It is done Column Wise - We take each column $(8$ bytes - $64$ Bits) of the State matrix and add them with the corresponding columns of the Round Key under addition modulus $2^{64}$

• The Column is arranged in Little Endian Form - Smaller Indexed Bytes are the Least Significant Bytes

• For instance, for a $128$ State Matrix $B_{128}$ and Round Key $K_{128}$ we do addition the following way.